Ton-functies: meer realistische weergave van de werkelijkheid dan CPB-modellen

CPB Raming

In CPB (2015) wordt de Ramingsonzekerheid in kaart gebracht middels fan charts. In dit document kwamen wij dit figuur met bijhorende toelichting tegen:

Figuur 1: Feitelijk EMU-saldo fan chart voor CEP

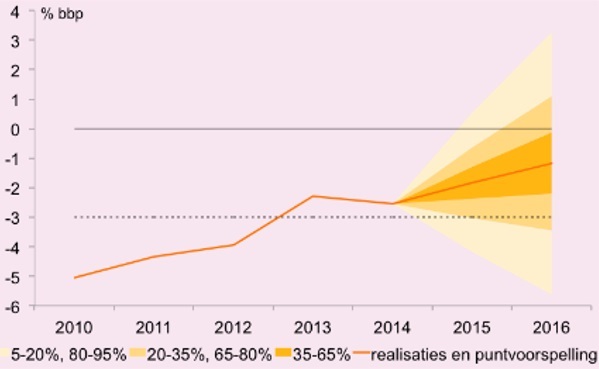
“De fan chart voor het feitelijke EMU-saldo is gevoelig voor het ramingsjaar 2009. In maart 2008 was de raming voor 2009 +1,4%. In maart 2009 waren de macro-economische gevolgen van de financiële crisis in het vizier en kwam de raming voor 2009 uit op -2,8%. De uiteindelijke realisatie voor 2009 werd echter -5,6%. Zonder het ramingsjaar 2009 zouden de standaarddeviaties voor het feitelijke EMU-saldo aanzienlijk lager zijn geweest en de bandbreedtes van de fan chart aanzienlijk smaller.” (CPB, 2015)

Economische realiteit in 2009

Om te begrijpen wat hier speelde, moeten wij even in herinnering roepen dat de economische realiteit van 2009 een geheel andere was dan die van de daarop volgende en zeker ook die van de daaraan voorafgaande jaren. Vóór 2009 was de liquiditeit ruim; wie krediet nodig had en daar een goed verhaal bij kon vertellen, kon krediet krijgen. Bedrijven en banken werden door markt en marge gestuurd. Zolang de marge goed was, waren langere betalingstermijnen acceptabel en werd het benodigde werkkapitaal door de bank verschaft; en de bank kon deze lening, na hem al of niet aan marktvereisten te hebben aangepast, weer doorverkopen. Het liquide Paradijs was op de planeet Aarde neergedaald.

Rond 2009 was de situatie een geheel andere. Bijna nergens kon nog tegen draagbare voorwaarden geld worden geleend. Het verkorten van de balans was voor veel bedrijven en instellingen een voorwaarde van overleving. Niet markt en marge, maar het verkrijgen van cash stuurde bedrijven en banken. Als maar geld op tafel kwam, accepteerde bedrijven zelfs lage of zelfs negatieve marges bij het verkopen van voorraden. Investeringsprojecten werden niet langer geëvalueerd naar hun netto contante waarde, maar naar hun liquiditeitsbehoefte. Kasbeheer zat bij de directies prominent aan tafel. De terugval in winst en omzet werd in veel gevallen beschouwd als het minste kwaad, met alle gevolgen voor de fiscus van dien. De monetaire autoriteiten reageerden op deze situatie door gigantische hoeveelheden geld in de economie te pompen, en wel zodanige hoeveelheden dat het kasbeheerders gemakkelijker werd gemaakt om in de liquiditeitsbehoefte van hun bedrijf of instelling te voorzien. Geleidelijk werden marge en omzet weer leidend en werd liquiditeit weer een technische puzzel – op te lossen tussen kasbeheer en bank.

Ton-functie

De beschrijving van een economie waarin op een bepaald moment een variabele wordt gelimiteerd door de ene (markt en marge) en op een ander moment door de andere (liquiditeit) restrictie, vergt een ander model dan dat zoals in dit geval werd ontwikkeld door het Centraal Planbureau. Dat model is niet geschikt en resulteert in een onnodige toename van de standaarddeviatie. De voorspelde waarden worden minder nauwkeurig. Het probleem zit, wat ons betreft, niet in de onvoorspelbare wispelturigheid van de economie, maar in een model dat die realiteit niet goed weergeeft – sterker nog: niet goed kan weergeven.

Wij stellen ons voor dat de oplossing moet worden gezocht in het ontwikkelen van een geheel ander model, weerspiegeld in de zogenaamde de “ton-functie” (“barrel function” in het Engels). Deze naam is begrijpelijk na het zien van bijgaande tekening (zie Figuur 2). Deze is geleend van een principe (de wet van Liebig) dat vaak wordt waargenomen in de plantenfysiologie. Deze wet stelt het volgende: de groei van een plant wordt bepaald, niet door de totale hoeveelheid beschikbare voedingsstoffen, maar door die voedingsstof die het meest schaars is in relatie tot de behoefte van de plant (de beperkende factor). Dit verschijnsel wordt gevisualiseerd in het beeld van een waterton met duigen van verschillende lengte, die vaak de ton van Liebig wordt genoemd. Zoals de capaciteit van zo’n waterton wordt bepaald door de kortste duig, zo wordt de groei van de plant gedetermineerd door de voedingstof die in relatie tot de behoefte van de plant het meest schaars is. En zoals de lengte van de overige duigen geen invloed heeft op de capaciteit van de ton, zo heeft de beschikbaarheid van de andere voedingsstoffen geen invloed op de groei van de plant.

Parallel hieraan kan worden gesteld dat van een “ton-functie” sprake is als een functie bestaat uit een combinatie van meerdere sub-functies, en het resultaat niet wordt bepaald door een combinatie van sub-functies, maar slechts door één – de limiterende functie. De overige functies spelen geen rol bij het bepalen van de uitkomst en zijn “onzichtbaar” of “slapend” totdat de limiterende sub-functie ophoudt limiterend te zijn en een andere sub-functie deze rol overneemt. Wiskundig kunnen deze ton-functies eenvoudig worden beschreven als:

x_t = MIN(f(a_t, b_t, c_t ….);g(….y_t, z_t);…..).

In het geval van ons voorbeeld zou het “gewone” beeld (bepaald door markt en marge) weergegeven worden door f(a_t, b_t, c_t….) en de crisis (waarin het EMU-saldo wordt bepaald door de beschikbare liquiditeit) door g(….y_t, z_t). Wanneer de crisis toeslaat, is de eerste sub-functie (om terug te vallen op de regenton) de langste duig, terwijl onder “gewone” omstandigheden de tweede sub-functie langer is. De lengte van de langste duig heeft geen invloed op de hoeveelheid water die de ton kan bevatten. Die duig/sub-functie “slaapt”. Het is de duig die op een bepaald moment de kortste is die de dat bepaalt.

Het EMU-saldo is bij lange na niet het enige economische fenomeen dat het meest realistisch met een ton-functie kan worden beschreven – integendeel. Ton-functies zijn vooral toepasbaar waar invloedrijke variabelen elkaar zeer moeilijk of geheel niet kunnen vervangen – met andere woorden: waar de onderlinge substitueerbaarheid gebrekkig is of geheel ontbreekt. Zo is het niet onmogelijk dat in landen ingesloten in de Sahel in drogere jaren de regenval (via voedselbeschikbaarheid) bepalend was voor de welvaart, terwijl in jaren waarin voldoende of zelfs teveel regen viel die regen verder geen invloed had. De bevolking kan geen spijkers eten en evenmin met rijst en sorghum huizen bouwen. Een ander voorbeeld in de economische literatuur is de “jack-of-all-trades”-theorie in de arbeidseconomie: het succes van een werknemer of ondernemer wordt gedetermineerd door de vaardigheid die hij of zij het slechtst heeft ontwikkeld (Spanjer & Van Witteloostuijn, 2017 en Malinvaud, 1977).

In zijn boek “Economics Rules” stelt Dani Rodrik (2015) dat nu eens het ene, dan weer het andere model de werkelijkheid goed lijkt weer te geven, en dat de keuze van het op dat moment in die context “correcte” model een wezenlijk deel van het economen vak is. Deze keuze is zijns inziens meer ambacht, intuïtie en ervaring dan wetenschap. Wij stellen daar tegenover dat wat hij modellen noemt, in wezen sub-functies zijn – met andere woorden: onderdelen van wat als ton-functies geformuleerd kan worden. Hij schuift “niet toepasselijke” modellen ter zijde voor een mogelijk toekomstig gebruik; wij stellen dat modellen (als zij valide zijn) regelmatig een tijdje “slapen”(niet limiteren), en dat de econoom in het formuleren van de ton-functie expliciet moet maken wanneer zij “wakker worden” (wel limiteren): Niks ambacht, intuïtie of ervaring, maar harde analyse.

Conclusie

Wij erkennen dat de aanpak van Rodrik, vergelijkbaar met de stylering van Tinbergen, statistische en mathematische analyse vergemakkelijkt. Maar door onze aanpak wordt het CPB-model, waarmee wij dit artikel begonnen, significant nauwkeuriger. Immers: het jaar 2009 – waarin niet de sub-functie markt en marge, maar de sub-functie financiële crisis limiterend zou zijn – zou niet meer verstorend werken. Bovendien worden onderzoekers dan gedwongen om een poging te wagen de risico’s op een nieuw 2009 in te schatten, en deze in hun voorspelling (inclusief de “fan chart”) in te bouwen. Dit zou resulteren in een veel smallere “fan”, met een losse “taartpunt” schuin naar beneden. De kleur van deze laatste zou de inschatting van het CPB weergeven van de kans dat wederom een financiële crisis optreedt, terwijl de hoek naar beneden de inschatting van de door het CPB verwachte gevolgen aangeeft. Daarmee zou het realiteitsgehalte van gemelde “fan chart” aanzienlijk toenemen, zelfs als de onzekerheden rond deze inschattingen voorlopig nog bijzonder groot zullen zijn.

Referenties